Preis-Absatz-Funktion

4.2.1.2 Erlös-, Grenzerlösfunktion

Cournotscher Punkt

er Begriff Grenzumsatz (oder Grenzerlös) wurde im Abschnitt über die direkte Preiselastizität der Nachfrage eingeführt. In der Unternehmung bei vollkommener Konkurrenz ist der Grenzumsatz immer gleich dem Preis, denn jede weitere abgesetzte Einheit lässt den Umsatz jeweils um den Marktpreis ansteigen. Infolge des unbedeutenden Marktanteils wirkt sich die Ausweitung des Absatzes nicht auf den Preis aus.

In der Monopolunternehmung sieht das anders aus. Zwar lässt eine weitere abgesetzte Einheit den Umsatz über den Mengeneffekt ansteigen, zugleich aber drückt die größere Absatzmenge den Preis nach unten, wodurch ein negativer Preiseffekt entsteht. Für den Umsatz des Monopols gilt wie für jede andere Unternehmung auch

$$ U = p \cdot x \tag{1} $$

Die Veränderung des Umsatzes kann angegeben werden mithilfe des totalen Differentials

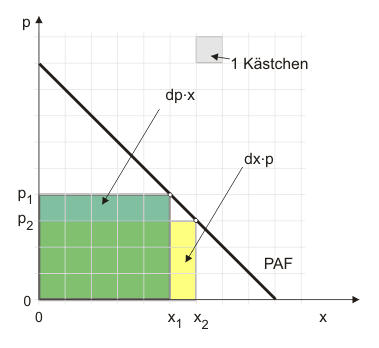
$$ \text{d}U = \text{d}p \cdot x + p \cdot \text{d} x \tag{2} $$ $$ \text{d}U = \text{d}p \cdot x_1 + p_2 \cdot \text{d} x \tag{3} $$

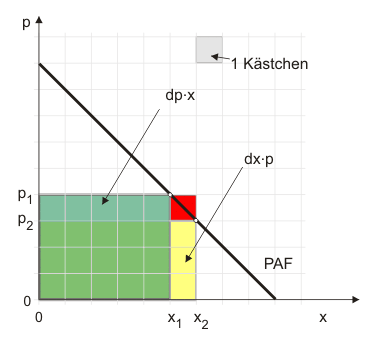
Genau genommen wird die Veränderung des Umsatzes zwar mit der Menge der Ausgangssituation $x_1$, aber nicht mit dem Preis der Ausgangssituation  $p_1$ berechnet. Um den Fehler zu ermitteln, den man mit (2) macht, wird $p_1 \cdot \text{d} x$ zu (3) addiert und gleich wieder subtrahiert:

$$ \text{d}U = \text{d}p \cdot x_1 + p_2 \cdot \text{d} x + \text{d}x \cdot p_1 - \text{d}x \cdot p_1 \tag{4} $$ $$ \text{d}U = \text{d}p \cdot x_1 + \text{d}x \cdot p_1 - \text{d}x \cdot p_1 + p_2 \cdot \text{d} x \tag{5} $$ $$ \text{d}U = \text{d}p \cdot x_1 + \text{d}x \cdot p_1 + \text{d}x(p_2 - p_1) \tag{6} $$ $$ \text{d}U = \text{d}p \cdot x_1 + \text{d}x \cdot p_1 + \text{d}x \cdot \text{d}p \tag{7} $$

Der Unterschied gegenüber der Berechnung mit (2) beträgt also $\text{d}x \cdot \text{d}p$ Wenn $\text{d}x$ klein ist, wird auch die dadurch ausgelöste Preisänderung $\text{d}p$ klein sein, so dass $\text{d}x \cdot \text{d}p$ getrost vernachlässigt werden kann, wenn die Änderungen nicht allzu groß sind. Wenn Sie Abbildung 1 anklicken, wird $\text{d}x \cdot \text{d}p$ als rote Fläche gezeigt. 

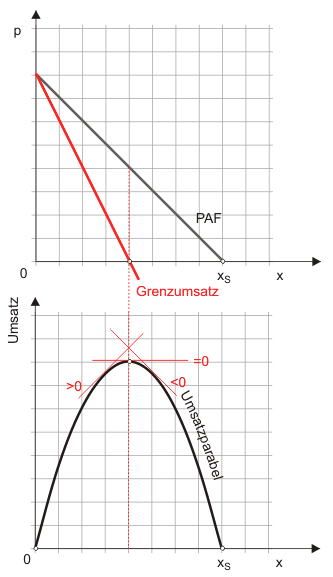
Ausgehend von einer linearen Preis-Absatz-Funktion soll nun die Grenzerlös- oder Grenzumsatzfunktion ermittelt werden. Zunächst wird die Umsatzfunktion aus den Flächen für alternative Preis-Mengen-Kombinationen unter der Preis-Absatz-Funktion  konstruiert. Dazu wird das entsprechende Diagramm aus dem Abschnitt über die direkte Preiselastizität der Nachfrage herangezogen Animation. Im Unterschied dazu sind in Abbildung 2 die beiden Teildiagramme allerdings vertauscht: Die Umsatzparabel ist nun im unteren Diagramm zu sehen. Außerdem wird die Nachfragefunktion nun Preis-Absatz-Funktion genannt.

  

Zur grafischen Bestimmung des Grenzumsatzes, der der Steigung der Umsatzfunktion entspricht, sind im oberen Teildiagramm drei rote Hilfslinien eingezeichnet, an denen man deutlich erkennt, wie der Grenzumsatz zunächst positiv, dann null und anschließend negativ wird. Der Umsatz ist offensichtlich maximal, wenn der Grenzumsatz null ist (notwendige Bedingung).

Außerdem macht die Abbildung deutlich, dass kein Monopolist im Bereich negativer Grenzumsätze anbieten wird. Jeden Umsatz, den man in diesem Bereich erzielen kann, kann man auch mit geringerem Absatz erzielen. Ein geringerer Absatz bedeutet aber eine kleinere Produktionsmenge, so dass bei gleichem Umsatz die Kosten vermindert werden können. Also wird der Monopolist nur im Bereich positiver Grenzumsätze anbieten. Mit anderen Worten:

Das folgt unmittelbar aus der Amoroso-Robinson-Relation $\cfrac{\partial U}{\partial x} = p \Bigl( 1 + \cfrac{1}{E_{x,p}} \Bigr)$, die die Grenzumsätze in Abhängigkeit von der direkten Preiselastizität der Nachfrage zeigt. Nur wenn $|E_{x,p}|>1$ zutrifft, ist der Grenzumsatz positiv. Zudem sei noch einmal daran erinnert, dass die Umsätze maximal sind, wenn $E_{x,p} = -1$. Dieses Ergebnis konnte hergeleitet werden, ohne eine spezifische Gestalt der Preis-Absatz-Funktion anzunehmen. Es gilt also generell. Das trifft auch auf die Aussage

zu, was einfach eine Folge davon ist, dass die Ausweitung des Absatzes den Preis fallen lässt. Der Absatz kann eben nur bei fallendem Preis ausgedehnt werden.

Den Beweis, dass die Grenzumsätze immer unter dem Preis liegen, liefert der  Wert des Klammerausdrucks in der Amoroso-Robinson-Relation. Man kann mit an Sicherheit grenzender Wahrscheinlichkeit einen positiven Wert der direkten Preiselastizität der Nachfrage ausschließen. Also ist der Klammerausdruck kleiner als eins und die Aussage bewiesen. Allerdings muss sie für einen Grenzfall eingeschränkt werden. Wenn die Elastizität gegen (minus) unendlich geht, stimmen Grenzumsatz und Preis überein. Das beschreibt aber gerade den Fall vollkommener Konkurrenz. Dieser Aspekt wird im Rahmen der Messung der Monopolmacht >wieder aufgegriffen.

Mit $a$ als Achsenabschnitt und $b$ als Steigungsmaß lässt sich die Preis-Absatz-Funktion schreiben als

$$ p = a - bx \tag{8} $$

Der Umsatz ist somit gegeben durch

$$ U = px = ax - bx^2\tag{9} $$

so dass für den Grenzumsatz GU (erste Ableitung der Umsatzfunktion)

$$ GU = U' = a -2bx \tag{10} $$

sofort abgelesen werden kann, dass der Ordinatenabschnitt $a$ mit dem der  Preis-Absatz-Funktion übereinstimmt und die Steigung mit $-2b$ doppelt so steil ausfällt. Wer sich das eingeprägt, kann sich zukünftig die Berechnung der Grenzumsatzfunktion sparen - jedenfalls wenn die Preis-Absatz-Funktion eine Gerade ist. 

Hätte der Monopolist keine Kosten ("Mineralwassermonopol")*, wäre sein Gewinnmaximierungsproblem bereits gelöst: Dehne die Produktion aus, bis der Grenzumsatz gleich null ist. Diese Aussage gilt nicht nur für eine lineare Preis-Absatz-Funktion, sondern allgemein. Allerdings ist noch die hinreichende Bedingung für ein Umsatzmaximum zu beachten. Die Grenzumsätze  müssen fallen.

Nach ähnlichen Seiten im WWW suchen